AM
Animated Mathematics
differentiation of x power n

First Principles Differentiation of xn

The derivative of f(x)=x2 was found to be f'(x)=2x. Here, the derivatives of higher powers of x shall be investigate to demonstrate a pattern. Note in the algebra shown below, Pascal's triangle is used to expand powers of (x+h)n.

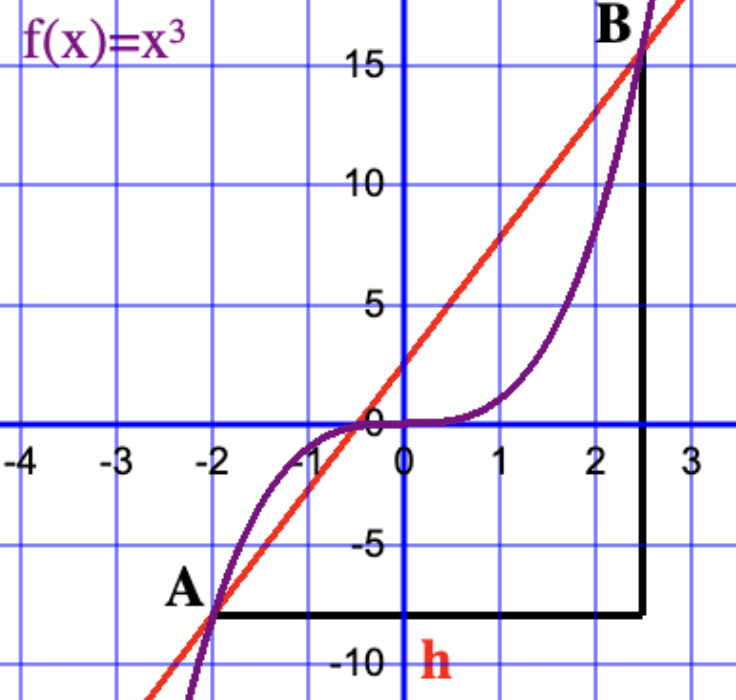
First Principles Differentiation of x3

The function f(x)=x3 is an antisymmetic function since f(x)=-f(-x), one can substitute x with some values to demonstrate this e.g. f(2)=8 and f(-2)=-8, therefore f(2)=-f(-2). A secant line passes through the points A(x,x3) and B(x+h,(x+h)3). f'(x) is found by taking the limit h → 0.

taking the limit animation for f(x)=x^3
calculus first principles f(x)=x^3 cubic
of the analysis.

First Principles Differentiation of x4

The function f(x)=x4 is a symmetic function since f(x)=f(-x), one can substitute x with some values to demonstrate this e.g. f(2)=16 and f(-2)=16, therefore f(2)=f(-2). A secant line passes through the points A(x,x4) and B(x+h,(x+h)4). f'(x) is found by taking the limit h → 0.

taking the limit animation for f(x)=x^4
calculus first principles f(x)=x^4 quartic
of the analysis.

First Principles Differentiation of x5

The function f(x)=x5 is an antisymmetic function since f(x)=-f(-x), one can substitute x with some values to demonstrate this e.g. f(2)=32 and f(-2)=-32, therefore f(2)=-f(-2). A secant line passes through the points A(x,x5) and B(x+h,(x+h)5). f'(x) is found by taking the limit h → 0.

of the analysis.

The results for f(x)=xn for n=2,3,4 and 5 suggests that the derivative f'(x)=nxn-1, let see if the pattern holds for a negative value of n.

First Principles Differentiation of 1/x

The function f(x)=x-1 is an antisymmetic function since f(x)=-f(-x), one can substitute x with some values to demonstrate this e.g. f(2)=1/2 and f(-2)=-1/2, therefore f(2)=-f(-2). A secant line passes through the points A(x,1/x) and B(x+h,1/(x+h)). f'(x) is found by taking the limit h → 0.

taking the limit for f(x)=1/x animation
algebra for derivative first principles 1/x
of the analysis.

Discussion

The table summarizes our findings for the derivative of f(x)=xn for several integer n values. The results suggests that the derivative of f(x)=xn is f'(x)=nxn-1 for integer values of n. The Binomial expansion can be used to prove that the result holds for all positive integer values of n. However, the derivative rule is valid for all real values of n, including negative, fractional, and irrational values; the proof is beyond the scope of this page.


f(x) f'(x)
x2 2x1
x3 3x2
x4 4x3
x5 5x4
x-1 -x-2
xn nxn-1