Integral Test and P-Series
Introduction
If we add an infinite series of numbers will the sum be infinite or a finite number ?. The series is said to diverge if the answer is infinite, and series is said to converge if the sum has a finite value such as a:
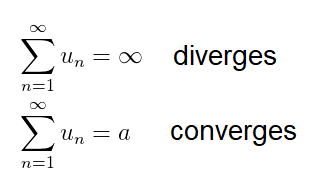
A student first encountering this concept can be forgiven for thinking that the sum of an infinite series is always infinite, since there are an infinite number of terms; however this is not true for an infinite geometric series which has the form:
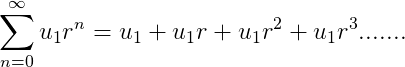
The sum of a geometric series is convergent provided ∣ r ∣ <1 where r is the common ratio. The latter restriction on r ensure that the next term in the series is small that previous term i.e.
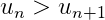
this however is not the condition for the convergence of all series. All decreasing series do not converges we study and compare the harmonic series which is the sum of the reciprical of positive integers
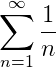
with the infinite sum of the reciprocal of the square numbers. Both series we shall see later are special cases of the p-series.
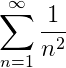
Calculating the Partial Sums
In the figure below the partial sums of the two series are calculated. When k=1 both series equal 1. The value of k can be increased or decreased using the buttons.
change k
The graph of the partial sums suggests that as k→∞ the harmonic series diverges and the other series converges to around 1.65. This is just numerical study and does not prove the convergence or divergence of either series.
Integral Test: Harmonic series 1/n1
The Harmonic series and the function f(x)=1/x are drawn on the same graph. The Harmonic series can be represented by either the left of right Riemann sums. The integral of f(x) is calculated below, and the area under f(x) (in the limit x→∞) is infinite.
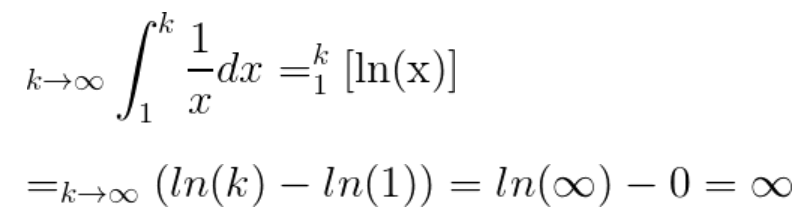
Riemann Sum
The Harmonic series even though it is a decreasing series diverges (i.e. the sum equals infinity); this is a counter intuitive results, but the comparision with f(x) proves it's divergence. Actually, indefinite integrals and the sum of series is full of counter intuitive results, which makes the subject so fascinating.
Integral Test: series of 1/n2
The Harmonic series and the function f(x)=1/x are drawn on the same graph. The Harmonic series can be represented by either the left of right Riemann sums. The integral of f(x) is calculated below, and the area under f(x) (in the limit x→∞) is infinite.
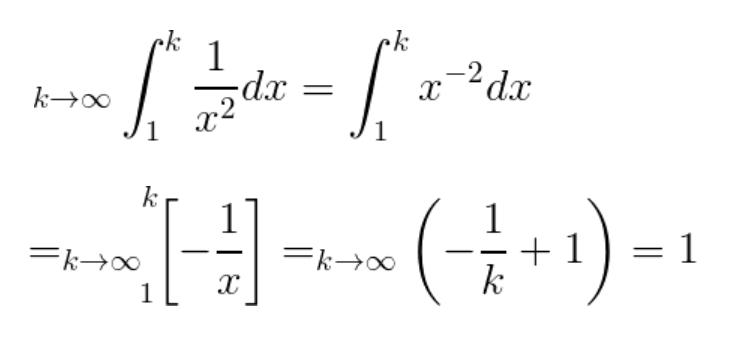
Riemann Sum
The integral test estimate the sum of the series to be smaller than 2, which concurs with the numerical estimate of around 1.65.
The Integral Test: formally stated
The integral test stated formally f(x) is a continuous, positive decreasing function in the interval [a,∞) and f(n)=un then
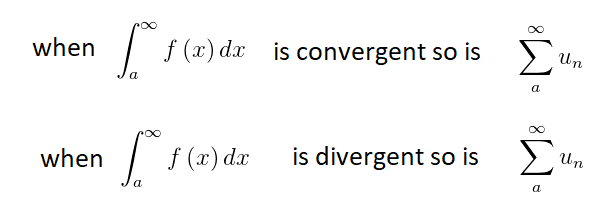
The P-series: sum of 1/np
The integral test can be applied the p-series which has the form:
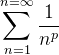
where p is a real number. We need to integrate the continuous decreasing function:
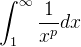
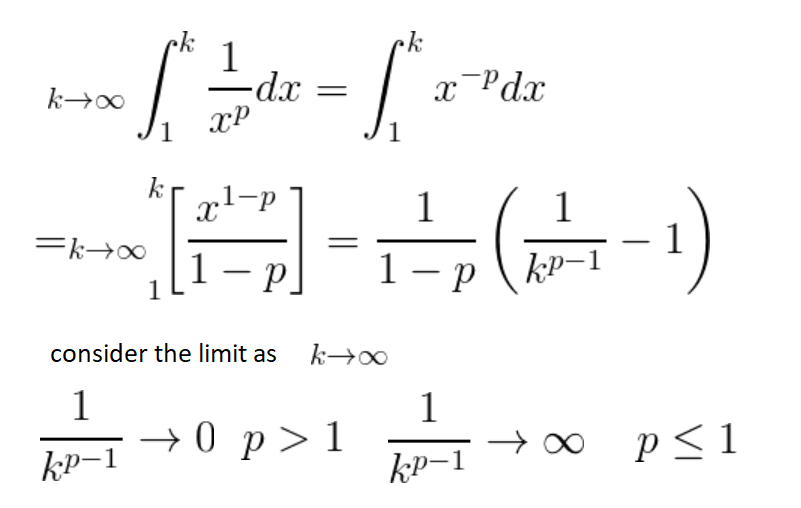
Therefore, we can conclude that:
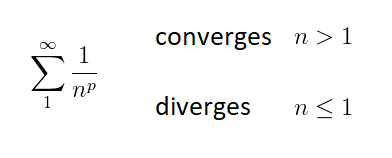
Integal test: Suitable functions
The function used in an integral test, must be eventually a decreasing function. The figure below shows the Riemann rectangles for a function that increases and then decreases. The Riemann rectangle are not consistently above/below the function, for example the left Reimann sums are above the function when it is decreasing and below the function when the function in increasing. Therefore, the integral test can only be used directly for the domain (i.e. range of x-values) for which the function is decreasing. The domain for which the function is increasing will add a finite number to the final sum. Therefore, the integral test can be used for function that are eventually decreasing and they can have a domain where it is increasing Another figure shows the Riemann rectangles for a function which is discontinuous at x=3.5 since it has a vertical asymptote. The function cannot be integrated when the integration limits contains a vertical aymptotes x=3.5, hence this precludes using the integral test for a function which is discontinuous.

