Differentiation From First Principles
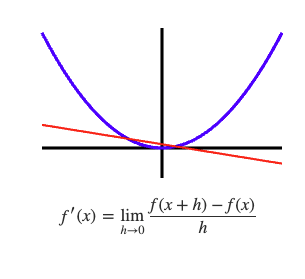
The aim of differentiation is to find the gradient of the tangent lines to a curve. A tangent touches the curve at one point, and the gradient varies according to the touching coordinate. The tangents of the function f(x)=x² can be explored using the slider below.
The Secant line Limit
The secant line crosses the function at two points A and B. The point A is kept fixed and the point B is moved towards A until it's at A. This process is known as taking a limit. Below (left) the limit is taken numerically where you can move the point B towards A, and you can also move the A coordinate. The gradient of the secant line is calculated using the rise over run concept . In practice the point B is placed very close to point A but it cannot have the same coordinate otherwise there will be a division by zero error in the calculation. The numerical answer however is very close to the correct answer, and sometimes aided by numerical accuracy limits the exact answer is fortuitously calculated. The exact value of the limit can be found algebraically (below right), and this involves some simple algebraic cancellation to circumvent a gradient equal to 0/0 which is an indeterminate form.
Finding the Limit B → A numerically
Finding the Limit B → A algebraically
The limit h→0 for A(x,x²) and B(x+h,(x+h)²)
In the above examples the limit is found where A coordinate is given a numerical value. Below the limit is calculated for A(x,x²) and B(x+h,(x+h)²). The limit h→0 can be visualised below by pressing "take limit"; this is what Newton imagined centuries ago, and I wonder he would make of the animation if he could see it. The limit as a function of x is found algebraically below right.
Example: find equation of tangent to the curve f(x)=x²
Find the equation of the tangent that touches the curve f(x)=x² at the point (1,1). Press the buttons to see the solutions, try your own solution before seeing the solution, did you get it right?
Discussion
The fundamental idea behind differential calculus seems simple enough and it is an elegant and powerful idea. In this page we have only discussed differentiation f(x)=x², and the next section shall discuss differentiating f(x)=xn. where n is a positive integer.
