Determining the Maximum and Minimum Points
We shall study a cubic polynomial f(x) constructed from the product of three linear terms; there are three solutions and two "stationary point" in this case the local maximum and minimum points. Differentiation can be used to find the coordinates of these stationary points and also can help to distinguish between the local maximum and minimum points.
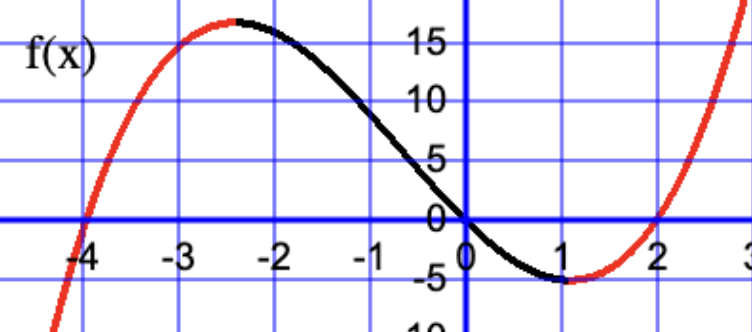
The increasing sections of f(x) is shown in red, and decreasing section is shown in black. When a continuous function f(x) is increasing the tangent line for a given x value is positive which means f'(x)>0. When f(x) is decreasing then f(x) is negative. press "animate tangent" and observe the gradient of the tangent line, and also observe the value of the tangent gradient shown in the lower graph.
When the f'(x)=0 the tangent line has zero gradient and is parallel to the x-axis. At the stationary points f'(x)=0, and we need find the x values who which f'(x)=0. You can press "next step" to see how this is determined. f'(x) is a quadratic function and the x values are calculated using the quadratic formula. A sign diagram is used to distinguish between the local minimum and maxiumum.
You can view a few examples. As a test find the stationary points yourself, and then check your answer by pressing the buttons
Summary
The table on the right summarizes our finds, and it's actually quite simple. f(x) is the y coordinate of a point for a given value of x. f'(x) on the other hand is the gradient of the tangent for a value of x.
| f(x) | f'(x) |
|---|---|
| point on line is (x,f(x)) | gradient of tangent for x |
| increasing | positive |
| decreasing | negative |
| turning point | 0 |
| maximum point test | + 0 - sign diagram |
| minimum point test | - 0 + sign diagram |
