TOK of Maclaurin Expansions
Introduction
Any event that creates knowledge usually involves most of the ways of knowing (WOKs) described in TOK. In this page we discuss the development of Maclaurin Expansions through a TOK perspective. The Maclaurin expansion started with the hypothesis that any function can be expanded in a power series:
The standard Maclaurin expansion formula is derived by repeated differentiation and then setting x=0:
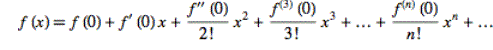
The above is a hypothesis and does not prove that the expansion is applicable for all functions. The Maclaurin expansion is an infinite series and in practice an infinite number of terms cannot be used. However, if the expansion starts to increasingly resemble f(x) as more terms are used then this suggests that the expansion "converges" to f(x). Note this does not prove that the expansion converges to f(x). This convergence can be studied using a computer. Before studying some common Maclaurin expansions consider the table below. The percentages must add up to 100%. The expansion was probably discovered independently by many people, and it's quite possible that they used their imagination to hypthosis the expansion. Perhaps, reason was the main driving force for the hypthosis. You can fill in the first line of the table below and explain your percentages. Do you think the person(s) who made the hypothesis had any idea which for functions the expansion converges.
| Knowledge Event | Reason | Sense Perception | Emotion | Faith | Intution | Imagination | Memory | Language |
|---|---|---|---|---|---|---|---|---|
| Expansion Hypothesis | ||||||||
| sin expansion | ||||||||
| exp expansion | ||||||||
| 1/(1-x) expansion |
Graphing Maclaurin Expansions
f(x)=sin(x) Maclaurin Expansion
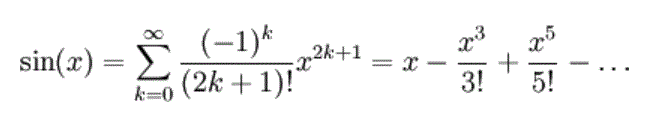
k=0
f(x)=exp(x) Maclaurin Expansion
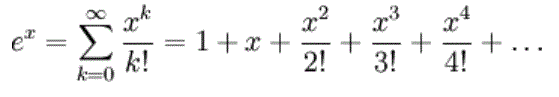
k=0
f(x)=1/(1-x) Maclaurin Expansion
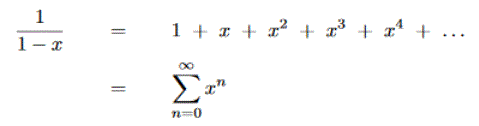
k=0
After investigating the Maclaurin expansions graphically do you think that the first two converge and for what domain (i.e. x values); do the graphical studies prove that a given series converges. The Maclaurin expansion of 1/(1-x) is really an infinite geometric series, therefore is it possible to prove the domain of convergence for it's Maclaurin expansion. Fill in the table for the three expansions after studying them graphically. The convergence of Maclaurin expansions can be studied rigorously using series convergence tests, and these shall be discussed in later pages.

