Vertical and Horizontal Lines
The sliders rotates the blue line which makes an angle with the horizontal x-axis.
The gradient m=0 for a horizontal line, and all horizontal lines have zero gradient. The sliders allows you to get closer and closer to 90 degrees in small incremental steps. This process is known as "taking a limit" and is represented by an arrow:
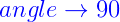
The value of the gradient m increases with the angle, and for angles close to 90 degrees even a change of 0.001 degrees causes a big change in m. The slider allows you to get up to 89.999 degrees which is enough to see the trend that as:
The gradient is the ratio "RISE/RUN. The "RUN" becomes smaller and smaller with angle and the RUN=0 when the angle=90 degrees. A finite number divided by zero is equal to infinity which is why a vertical line has an infinite gradient.
Equation of vertical and horizonal lines
The graph shows vertical and horizontal lines and the equations of these lines. The formulas for vertical and horizontal lines are simple since there are no m-value in the formulas.
All points on the horizontal line have the same y-coordinate. All points on the vertical line have the same x-coordinate.
Exercise: Draw vertical/horizontal line.
A simple exercise, use the slider and button to draw the line:
Intersection with vertical/horizontal lines.
The intersection of a vertical/horizontal line can be estimated by drawing both lines.
Press to see further examples with either vertical or horizontal lines:
The exact coordinate can be found by using algebra as follows:
Exercise: Find intersection with vertical/horizontal line
Determine the intersection coordinates of lines:
numerator denominator
numerator denominator
check your working out below:
Summary
(1) Vertical lines have infinite gradient. The equation of a vertical line has the form x=a, where a is a number.
(1) Horizontal lines have zero gradient. The equation of a horizontal line has the form y=a, where a is a number.

