Introduktion till Enhetscirkeln
Enhetscirkeln har radien 1 längdenhet och är centrerad i origo (0,0). Poängen P(x,y) kan vara var som helst på cirkelns omkrets. Linjen från origo till punkten P gör en vinkel med den horisontella x-axeln. Den värdig definitionen för \( sin \theta \) och \( cos \theta \) för vinklar \( \theta > 90 \) är x-koordinaten av P är lika \( cos \theta \) och y-koordinaten av P är lika \( sin \theta \) , därför \( x=cos \theta \) and \( y=sin \theta \), det är det definierande konceptet bakom trigonometri och ibland kan det vara förvirrande eftersom det är så enkelt.
Använd en miniräknare fär att beräkna sinus och cosinus fär vissa vinklar och jämför med x och y värdena i animationen. Kolla din räknare där siffrorna har avrundats till fyra decimaler. Från enhetscirkeldefinitionen av sinus och consinus functioner vi har:
cos(0)=1, cos(180)=-1, cos(90)=0, and cos(270)=0.
värdemängden för cosinus är: \(-1\leq cos \theta \leq 1 \)
sin(0)=0, sin(180)=0, sin(90)=1, and sin(270)=-1
värdemängden för sinus är: \(-1\leq sin \theta \leq 1 \)
I mänga matteböker skrivs \( \theta \) som x, och notera att x inte är x-axeln, var inte förvirrad.
Lösa för vinkeln \(\theta \)
Ett vanligt uppgift, för vilka vinklar \(\theta \) i intervallet \(0\leq \theta \leq 360 \) är \( cos \theta =k \) eller \( sin \theta=k \) när \(-1\leq k \leq 1 \).
prova frågan innan du trycker på den blå knappen
Exempel: lösa för \(\theta \) när:
Lösningen
Sammanfattning
P(x,y) är en pöeng på cirklens omkrets och \( x=cos \theta \) and \( y=sin \theta \) den värdig definitionen för sinus och cosinus för vinklar som är större än 90 grader.
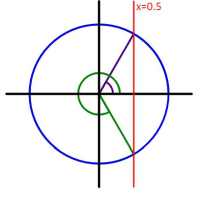
För att beräkna lösningarna på \( cos \theta =k \) visualisera skärningspunkterna för den vertikala linjen x=k med enhetscirklen. Den första lösningen får vi direkt genom att använda miniräknarens \( \theta=cos^{-1} k\). Den andra lösningen är reflektionen av den första lösningen genom x-axeln.
För att beräkna lösningarna på \( sin \theta =k \) visualisera skärningspunkterna för den horisontell linjen y=k med enhetscirklen. Den första lösningen får vi direkt genom att använda miniräknarens \( \theta=sin^{-1} k\). Den andra lösningen är reflektionen av den första lösningen genom y-axeln.
Du har gjort en utmärkt start på enhetscirklen om du förstår begreppen här.