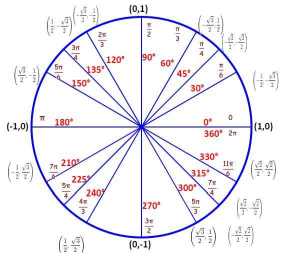
Introduction to the Unit Circle
The unit circle is a circle with radius r=1 and the point P(x,y) can be anywhere on the circumference. The line from the origon to the point P forms an angle with the horizontal x-axis. The unit circle allows for a formal definition for \( sin \theta \) and \( cos \theta \) for angles \( \theta > 90 \). The x coordinate of P is \( cos \theta \) and the y coordinate of P is \( sin \theta \) , i.e. \( x=cos \theta \) and \( y=sin \theta \). That is the fundamental concept behind trigonometry. Students often find this confusing at first because it is so simple.
The cos and sin functions of a scientific calculator accepts an angle and returns the x and y coordinates of the point P respectively. You can test your calculator with the unit circle on the left where the numbers have been rounded to 4 decimal places. The calculator should be in degrees mode. From the unit circle and the definition of cos and sin it follows that:
cos(0)=1, cos(180)=-1, cos(90)=0, and cos(270)=0.
The range of the cosine function is: \(-1\leq cos \theta \leq 1 \)
sin(0)=0, sin(180)=0, sin(90)=1, and sin(270)=-1
The range of the sine function is: \(-1\leq sin \theta \leq 1 \)
In most textbooks \( \theta \) is replaced by x, and note this x is not the x-axis of the unit circle, this can be another source of confusion.
Solve for the angle \(\theta \)
A common problem involving the unit circle is, solve for the angle \(\theta \) given \( cos \theta =k \) or \( sin \theta=k \) where \(-1\leq k \leq 1 \) and \(0\leq \theta \leq 360 \) .
Try the question before pressing to view the solution
Example: solve for \(\theta \) when :
The Solution
Summary
P(x,y) is a point on the circumference of the unit circle where \( x=cos \theta \) and \( y=sin \theta \), this is the formal defintion for the sine and cosine of angles that are greater than 90 degrees.
The solutions to \( cos \theta =k \) can be found by first visualizing the intersections of the vertical line x=k and the unit circle. The first solution can be found using the calculators arcos function. The other solution is then found by reflecting the angle through the x-axis.
The solutions to \( sin \theta =k \) can be found by first visualizing the intersections of the horizontal line y=k and the unit circle. The other solution is then found by reflecting the angle through the y-axis.
Understand the above and you have made a great start to the unit circle.